Kapitel 2:Vilka uppfattningar bör vi ha
Föllesdal Dagfinn, Wallöe Lars & Jon Elster
-Argumentationsteori, språk och vetenskapsfilosofi
1. Korrespondensteorin
Enligt FWJ (Follesdal, Wallöe, Elster) är sanning det vi försöker komma fram till
när vi bedriver vetenskapligt arbete: vi eftersträvar att våra uppfattningar ska vara sanna. För
att vara säkra som möjligt på att våra uppfattningar är sanna, försöker vi
finna skäl som talar för detta; vi försöker komma fram till uppfattningar som inte bara slumpmässigt
råkar vara sanna, utan är välgrundade, vi söker kunskap. Korrespondensteorin har varit i bruk sedan Platon (427-347 f Kr) (Föllesdal
m.fl. 1995: 36). Thomas av Aquino (1225-1274) och Bertrand Russell (1872-1970) var också förespråkare av korrespondensteorin (Föllesdal m.fl. 1995: 38). En proposition (eller en sats) är sann om den korresponderar mot fakta.
Ex. Påståendet ”Det snöar” är sant om och endast om det snöar.
Fråga 1.1: Vad är korrespondensteorin om sanning?
Svar 1.1: Sanning, enligt korrespondensteorin är ett mått på hur väl
ett påstående överensstämmer med verkliga förhållanden. Ett påstående är sant om det korresponderar (överensstämmer)
med det påståendet handlar om. Ett exempel på korrespondensteorin: “Det finns ca fem miljoner invånare
I Finland” är sant endast om utsagan stämmer överens med verkligheten. Denna teori ligger närmast
vår spontana uppfattning om vad sanning är.
Fråga 1.2: Vilka svagheter har korrespondensteorin?
Svar 1.2: Teorin har kritiserats för att den är svår
att tillämpa i matematiska sammanhang och för att den inte tar hänsyn till förnekande utsagor.
Ett problem med denna teori är att verkligheten bara kan beskrivas
i påståenden. Det finns ingen uppenbar gräns mellan verkligheten och våra beskrivningar
av den. Hur kan man hävda en överensstämmelse mellan ett påstående och ett observerat
faktum utan att beskriva faktumet i ord, så att det återigen blir ett nytt påstående, snarare
än den verklighet påståendet sägs handla om?
Generellt så är det stora problemet med korrespondensteorin att hitta ett sätt, alternativt förklara,
hur man avgör om ett påstående överensstämmer med det det handlar om (Föllesdal
m.fl. 1995: 39). En annan svaghet är också att våra åsikter får oss
att använda ett visst språk när vi beskriver verkligheten som i sin tur bekräftar korrespondensen.
2. Koherensteorin
Teorins klassiska formulering kommer från Spinoza (1632-1677) och Gottfried Wilhelm Leibniz (1646-1716). De var förespråkare
av denna syn på sanningen. Sanning, enligt koherensteorin är överensstämmelse
sinsemellan mellan idéerna i ett system (Föllesdal m.fl. 1995: 38). En proposition (eller en sats) är sann om den
har stöd i, eller är förenlig med, ett lämpligt koherent system. Det klassiska problemet är
att det kan finnas flera olika koherenta system, vilket t.ex. kan medföra att samma påstående
är båda sant och falskt.
Fråga 2.1: Vad är koherensteorin om sanning?
Svar 2.1: Enligt koherensteorin är "en uppfattning sann
om och endast om den passar in i en sammanhängande och allomfattande helhet av uppfattningar". Kunskap
blir ju då att känna till dessa uppfattningar samt hur de hör ihop (Föllesdal
m.fl. 1995: 38). Man avgör
om en sats är sann eller falsk genom något som kallas för sanningsvärde, eller koherensteorin
med ett finare ord. Med detta så kollar man om ett påstående hänger ihop logiskt med verkligheten
och inte är motsägelsefullt. Med hjälp av sitt förnuft förstår man att till exempel
4+2+5 blir 11 och det är bestående information, den är alltså koherent.
Fråga 2.2: Vilka svagheter har koherensteorin?
Svar 2.2: Teorin har kritiserats för att den inte klart och tydligt kan redogöra
för vad som menas med "sammanhang" mellan utsagor. Den menar att ett påstående är sant om det "hänger
samman" med alla andra sanna påståenden. En stark definition av koherensteorin menar att sanna
satser inte bara måste vara förenliga med andra sanna satser (d v s ej motsägande) utan även
måste impliceras av andra sanna satser (Föllesdal
m.fl. 1995: 39).
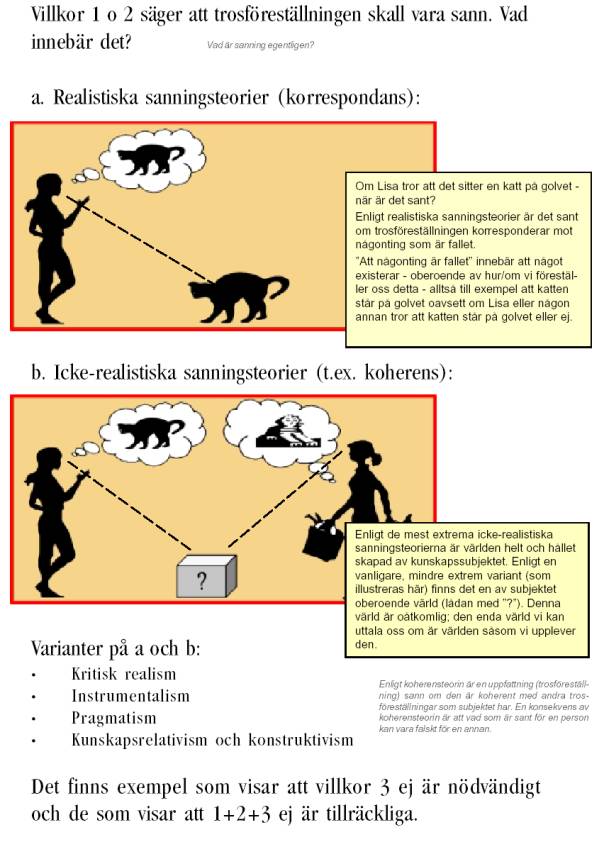
Ett exempel från Stockholms Universitets Psykologi hemsida som visar skillnaderna på de olika sanningsteorierna
[1]:
3. Kunskap
Det finns tre krav på kunskap. Att något vi tror är sant, betyder inte att vi har kunskap.
Vi kan tex. tro att fruktskörden på Österlen är stor i år, och därefter läsa
i tidningen att så är fallet. Vår tro visade sig alltså vara sann tro. Men den kan ha grundat
sig på en ren gissning, eller på mycket bristfällig information, tex. att vädret på
Österlen har varit bra i sommar. För att vi ska ha kunskap måste vår tro, förutom att
vara sann, vara välgrundad. För att en person, A, ska veta något, låt säga ´P`,
där ´P` tex. står för `fruktskörden på Österlen är mycket rik i år`,
måste därför tre krav vara uppfyllda (Föllesdal
m.fl. 1995: 44).
Kunskap är alltså samma sak som sann, rättfärdigad
tro enligt denna uppfattning (Platon, Aristoteles, Descartes, empiristerna formulerade dessa tre krav). (Föllesdal m.fl. 1995:
45).
Fråga 3.1: Hur lyder den klassiska definitionen av kunskap som innehåller de tre kraven?
Svar 3.1: Kunskap är sann, välgrundad
tro enligt författarna och de tre kraven som måste uppfyllas följer nedan:
Mer långrandigt:
För att A skall kunna sägas veta P, måste
• A tro P
• A ha goda skäl att tro P
• P vara sant
(Föllesdal m.fl. 1995: 44-45).
Till exempel:
1. Per tror att
katten jamar
2. Katten jamar
3. Per hör
jamande ljud från samma ställe där han ser en katt.
Katten ser ut
som om den jamar.
Katten står
framför en stängd dörr.
Katten brukar
jama framför stängda dörrar.
Man kan visa att
alla dessa krav är nödvändiga
för att man skall kunna prata
om ”kunskap”
[1]
4. Lögnarparadoxen
Författarna beskriver en typ av problem som dyker upp i alla sanningsteorier och som måste
lösas för att vi ska få en tillfredställande förståelse av sanningsbegreppet, är
de paradoxer som uppstår i sammanhanget. Typiskt för dessa är "lögnarparadoxen"
eller "Lögnaren" som sysselsatte filosoferna redan i antiken. Paradoxen beröres även i
Nya testamentet, där Paulus i sitt första brev till Titus, kap. 1, verserna 12-13, säger:
En av dem, en profet av deras eget folk, har sagt: "Kretensarna, lögnare jämt,
äro odjur, glupska och lata." (Föllesdal m.fl. 1995: 40).
Den första tydliga formuleringen av lögnarparadoxen tillskrivs Eubulides
(samtida med Aristoteles): En person säger "Jag ljuger nu." Om påståendet är sant så följer att det är en
lögn, d v s, det är falskt. Om påståendet är falskt så ljuger inte Eubulides utan
talar sanning, vilket betyder att hans påstående är sant. Först 1933 lyckades den polske logikern Alfred Tarski (1902-1983) formulera
en teori om sanning som inte leder till denna eller andra besläktade paradoxer. (Föllesdal
m.fl. 1995: 41).
En modernare version av paradoxen är: Denna sats är falsk (Föllesdal m.fl. 1995: 41). Tar vi satsen "Denna sats är falsk" får vi "Denna sats
är falsk" är sann om och endast om denna sats är falsk. Detta kommer dock leda till en självmotsägelse
varför definitionen inte är användbar.
Tarskis lösning var att föreslå att man skiljer mellan språk och metaspråk, där
bara metaspråket får uttala sig om sanning och falskhet hos satser i språket. (Föllesdal m.fl. 1995: 42).
Fråga 4.1: Hur uppkommer lögnarparadoxen enligt Tarski?
Svar 4.1: Tarski visade att dessa paradoxer nödvändigtvis uppstår i alla språk i vilka
logikens vanliga lagar gäller, och som är vad Tarski kallade " semantiskt slutna", det vill
säga att alla satser som säger att satser i språket är sanna eller falska själva tillhör
språket. Tex: När satsen "snö är vit" förekommer i ett semantiskt slutet språk,
så förekommer även satsen "`snö är vit´ är sann" i det språket.
(Föllesdal m.fl. 1995: 41).
Fråga 4.2: Hur löser Tarski paradoxen?
Svar 4.2: Tarski menade att vi måste skilja på objektsspråk och metaspråk.
"Ett motsägelsefritt språk, säger Tarski, får inte vara semantiskt slutet: det får
inte innehålla uttrycksmedel för att formulera språkets egen semantik. Dess semantik skall endast
kunna formuleras i ett metaspråk som beskriver det ifrågavarande språket, vilket i detta sammanhang
kallas objektsspråket." Om man inte gör det, uppstår paradoxer som lögnarparadoxen.
Satsen ´snö är vit´ tillhör objektspråket, medan
satsen "´snö är vit´ är sann" tillhör metaspråket. Vill man om
den sistnämnda satsen påstå att den är sann, måste man gå över till ett
meta-metaspråk. "´Snö är vit"´ är sann´ är sann", tillhör
alltså meta-meta språket, osv. (Föllesdal m.fl. 1995: 42). Ett annat exempel är: Barberaren rakar sig själv och rakas inte
av en barberare.
5. Axiomatiska metoden
Historiens mest inflytelserika
axiomatiska system konstruerades emellertid av en grekisk matematiker som hette Euklides. Euklides sammanfattade
sin tids matematiska vetande i ett stort arbete Elementa. Han utgick från ett fåtal definitioner av begrepp samt
från ett antal axiom, grundläggande, självklara sanningar. Från axiomen härledde han
sedan en stor mängd teorem, t.ex. det berömda Pytagoras teorem. (Föllesdal m.fl. 1995: 51).
Den axiomatiska metoden har sedan antiken framstått som den
bästa bevismetod som finns. Anledningen till detta är lätt att förstå. Axiomen bör
väljas så att det inte kan råda några tvivel om deras sanning. Euklides utgår från
10 axiom. (Fem av dem kallar han postulat, men de är av samma karaktär som axiomen). Några exempel
på axiom:
1. Man kan alltid dra en rät linje från en punkt till en annan.
2. Varje begränsad linje kan förlängas obegränsat.
3. Kring en medelpunkt kan man alltid beskriva en cirkel med en bestämd radie.
4. Alla räta vinklar är lika.
5. Storheter som täcker varandra är lika stora.
6. Det hela är större än sin del.
Det fanns dock ett problem med denna metod.
En noggrann analys har visat att Euklides, säkerligen omedvetet, ibland använde antaganden som han inte
explicit formulerat. När han gjorde slutledningar förlitade han sig på intuitiv logik. Det fanns
sålunda ett visst spelrum för tolkningar och misstag.[3]
Nedan beskriver jag de viktigaste begrepp som
används inom den axiomatiska metoden:
Fråga 5.1: Vad innebär den axiomatiska metoden?
Svar 5.1: Axiomatisk metod innebär att man härleder alla sanna satser från
axiom inom ramarna för ett axiomatiskt system, som betyder att alla sanningar är deduktiva, d v s de
är nödvändigt sanna. Detta är attraktivt därför att man då kan kräva att
kunskap är deduktivt sann, och det finns inte utrymme för tveksamheter.
En klassisk svårighet med axiomatisk metod är att identifiera eller enas om axiomen. När ett axiomatiskt
system visar sig leda till slutsatser som är "oacceptabla" reviderar vi axiomen. Det verkar alltså
som om vi testar axiomen mot något annat. Men då är de ju inte axiom i den bemärkelse som
först åsyftades, eftersom de uppenbarligen inte är självklara sanningar (och konventioner
förändras).
En begränsning i axiomatisk metod är att man inte kan härleda allmänna lagar om företeelser
i omvärlden, vilket är vad vetenskapen strävar efter. Det finns inget sätt att logiskt härleda
från en observation av ett enskilt förhållande att något gäller för en mängd
likartade förhållanden. Det blir en induktiv slutledning. (Föllesdal m.fl. 1995: 49-51).
Referenser:
- http://www.psychology.su.se/units/gu/pk/handoutsvt05/kap01.pdf
- Föllesdal Dagfinn, Wallöe Lars & Jon Elster, Argumentationsteori, språk och vetenskapsfilosofi,
1995
- http://www.math.uu.se/~lal/kompendier/Geometribok.pdf
